10月 12 2008
時間と別れるための50の方法(43)
●ψ*6上でψ5はどのように見えるのか――位置の等化の風景
わたしが自分の周囲に広大な空間の広がりを意識しているとき、その広がり自体が人間の内面*としてのψ*6になっているということを前々回にお話しました。このとき実際に見えている人間の外面としての知覚球体=ψ5自体は、何度も言うように奥行きが同一視されることによって超ミクロの微小領域の中に3次元球面として丸められており、ψ*6が意味する時空の原点Oに貼り付いたようにして入り込んでいます。
このように、次元観察子という概念を通して見ると、僕らが普段「わたしを中心とする空間の広がり」と何気に称している空間は「わたし」を規定するψ5と、「わたし」からの広がりを規定するψ*6が二重に重なり合うことによって成り立っていることが分かってきます。ヌーソロジーの考え方からすれば、前者は哲学者たちが実存(知覚の場所)と呼んでいるもの、後者は科学者たちが実存(物質の場所)と呼んでいるものにとても似ていると言えます。
また、このような空間の二重性を前提におくことによって、「現時刻」という瞬間性の中にすべての時間が集約された形で現象化している人間の意識の在り方をうまく説明することができるようになります。つまり、周囲の空間を時空=ψ*6として捉えているときには、その中心点では刻一刻と時間が刻まれ、毎瞬、毎瞬という点時刻があたかも車窓から見る風景のようにあっと言う間に過去へと流れ去って行き、その反対に周囲の空間を自分自身=ψ5として捉えたときは、そこでは過去、現在、未来へと至る時間はすべてその知覚球体の直径の中に4次元空間として凝縮されおり、そこには、永遠の現在が現れるというからくりになっているわけです。人間の意識において、瞬間と持続が「今」という現象において重なり合い、想起や直感がつねに「現在」として起こるのも、人間という存在が4次元時空と4次元空間が持つこのような二重性の接点として存在させられているからでしょう。
さて、時空*=ψ*6の原点にこうして知覚球面=ψ5が貼り付いているとするならば、僕らが時空として世界を眺望したとき、周囲の風景のいたるところに知覚球面が張り付いていても不思議ではありません。原点とは単に便宜上定められたものであって、時空上のどの位置であろうが原点となり得るからです。たとえば、3日前のこの同じ時刻にもわたしはこの椅子に座っていたとします。その時間を原点と考えれば「いつでも今」としての知覚球体はその3日前に移動していることになります。このときは文字通り主体が三日前にタイムトラベルを行っているわけです。物理的に言えば、当然、そのときの光は3光日(光速度で進んで3日かかる距離)の彼方に飛び去っていることでしょうが、奥行き方向はψ5においては常に同一視されているわけですから、知覚球体自体は時間の経過に対して何の影響も受けません。
では、空間的な移動の方はどうでしょうか。あそこに見えるビルの屋上を時空の原点としよう、と思えば、そこに「どこでもここ」の知覚球体は一瞬にして移動することが可能です。もっとも、このときは時間の移動とは違って、3次元球面として表された知覚球体内部では、原点の空間的移動(x,y,z方向への並進運動)に伴って3次元球面上でそれぞれの3方向への回転が起こることになります。しかし、知覚球体自体としての3次元球面自体はやはり全く同一のものです。
つまり何が言いたいのかと言うと、知覚球体(3次元球面とその自転軸)としての「自己=ψ5」が「いつでも今、どこでもここ」としての存在ならば、時空認識の中ではあらゆるところに偏在することができるということです。となれば、時空上のすべての点は客体であると同時に主体と呼んでいいものになります。このことは、「真の主体は客体の中に息づいている」というベルクソンの達観の幾何学的説明に相当していますが、こうした「遍くわたし」の様子を『人神/アドバンストエディション』では空海の言葉を借用して「即身」と表現しました。
重々にして帝網のごとくなるを即身と名づく――空海が『即身成仏義』で著したこの言葉は華厳経に登場するパールネットワークのイメージを彷彿とさせます。重々帝網とは、いかなる部分にも全体が映り込み、無際限にその像が反射し合っているような状態のことを言います。今風に言えばホログラフィーやフラクタルのイメージです。即身成仏というと、物質概念にまみれた僕らはすぐに即身仏を連想して、お寺の中でミイラ化しているお坊さんを連想しますが、空海が説いた意味は全く違います。もともとサンスクリッド語での「成仏(アビサンボーディ)」という言葉は「仏に成る」ということではなく、「仏である」ことの意で、仏であることとは「現等覚(げんとうかく)」のことであるとされています。現等覚とは読んで字のごとく「あらゆるものが等しいものとして見える」ということです。いわゆる差取り(悟り)ですね。まさに、重々帝網の風景とは、いつでも今、どこでもこことしての、即身成仏の姿そのものであるわけです。
ヌーソロジーではψ5が人間の意識に顕在化を起こした状態を「位置の等化」と言いますが、この状況はまさにこの空海が語った「即身成仏」の風景に酷似しています。主体の位置と客体の位置が同一のものに感じられてきたとき、世界はどのように見えなければならないか——それはまさしく空海が言うように、世界のあらゆるところに世界自身が重々帝網を為して映り込むということです。しかし、こうした描写だけではまだ自我の拠点たる時空概念を解体させるほどの意味の強度は生まれません。見るものは見られるものである、主体は客体の中にいる、これら過去の神秘家や哲学者たちの達観が人間の意識を変えるだけの力を持てなかったのも、その意味の強度に不足していたからだと言えるでしょう。問題はこうした達観をどのようにして僕らの現実的な知識に接続させていくかということなのです。——つづく







10月 22 2008
時間と別れるための50の方法(46)
●メビウスの帯とスピノール………(2)
前回からのつづき——まず、リボンを用意し、その両端ををリング状につなげます。リボンの中央上に任意の1点Sをとり、その外面側と内面側をそれぞれ点s、点s*とします。ここで外面側であるs点と内面側であるs*点を左の親指と人差し指で軽くつまみます。この「つまみ」は、点Sがこのリボンの内面と外面の両面にある点sと点s*による挟み込みによって与えられているということを意味します。ここで、リングに沿って二本の指を点Oを中心に回転するように滑らしていきます。180度滑らしていくと、スタート地点の反対側にまできますが、そこで二本の指を見ると、相変わらず外面側に親指、内面側に人差し指が添えられているのが分ります(下図1)。まぁ、当たり前の話ですが、これが通常の3次元空間での回転の性質です。
次にスピノール空間の場合を考えてみます。スピノールの回転する空間ではスタート地点と回転中心Oを挟んだ反対側の位置では外面と内面の関係が互いに捻れ、S(+∞、-∞)がS*(-∞、+∞)となっていました。3次元空間では無限遠点と云えども4次元空間上ではただの点にすぎませんから、+∞、−∞二つの無限遠点をそれぞれs、s*と置いてみましょう。すると4次元空間においては、点S(s、s*)を指し示しているスピールが半回転する間に、このリング自体がちょうど180度の捻れを作り、点S*(s、s*)を指しているということになります。そして、元の位置に戻ってくるまでにもう180度の捻れを作っており、早い話が、スピノールが回転によって次々と指し示して行く円環の位置はスピノールが一回転する間に360度の捻れを持っているわけですです。このことからスピノールの一回転が描く軌跡は二回捻りを入れたメビウスの帯と同じ形をしているということになります(下図2)。
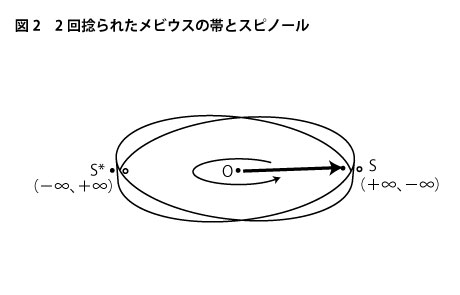
前回の図2で示したように、通常のメビウスの帯の場合は一回しか捩じれていないので、一回転回ってきたときに、表裏の関係が入れ替わりますが、二回捻れでは、半回転でそれが達成されるわけです。ということは、通常のメビウスの帯を2回巡ってくることと二回捻ったメビウスの帯を一回巡ることは、全く同じ意味合いを持っていることが分かります。つまり、1回捻れのメビウスの帯状の720度回転が2回捻れのメビウスの帯状の360度回転に対応しているわけです。通常の空間の回転角度をθとすれば、スピノールの空間の回転はθ/2でθを実現させます。
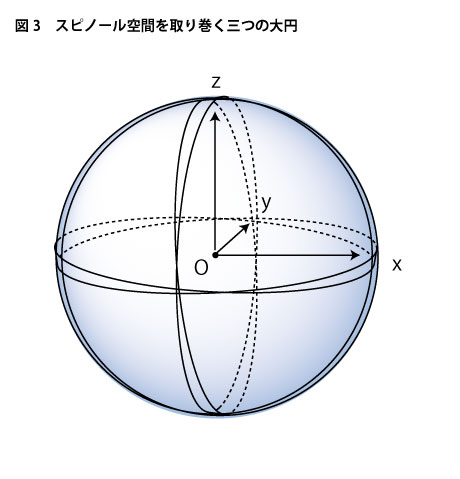
このような描像を持つことによってスピノールが張られた球空間の形がそれなりに輪郭を持ってきます。つまり、このスピノールが活動している球空間においては、このような円環構造が下図3のようにx、y、zの3方向すべてにおいて成り立っているわけです。はてはて、これは一体どんな形なのでしょう。
ここまでスピノールの回転の描像について見てきました。ヌーソロジーで見れば、4次元空間上でS(+∞、-∞)とS*(-∞、+∞)として対峙し合うのはψ5とψ6、つまり自己と他者の位置です。ここで『人神/アドバンストエディション』にも登場した「背中合わせの自己と他者」という関係を思い出してみて下さい。それらは同じ無限遠点±∞で背中同士でくっつき合っていました。つまり同じ位置にいるのです。ただ、自他では互いに向いてる方向が逆なので、前後方向が相互に逆になっています。つまり、点SとS*は同じ位置とも言ってよいのですが、冒頭に挙げた親指と人差し指の鋏み込みのように、一点を表裏の2点で指定しているために、その表裏の方向性の在り方によって二通りの組み合わせが出てきてしまうのです。このことは、図2に示したスピノールの回転が作り出す円環における二つの極点SとS*の位置も実は互いに重なり合って繋がっているということを意味しています(図ではそうは見えませんが繋がっていると考えて下さい)。つまり、回転中心O点からS点までを結んでできるスピノールはそのまま反対の極のS*点につながり、S*点からまた中心のO点に戻ってくるような円構造を持っているということです。このスピノールの回転が作る円の内部と外部をもし反転させて見ることができれば、二つのスピノールが一点を挟み込むようにして指定している様子が伺えることでしょう。
ということは、結局のところ、スピノールが張られている空間のかたちは3次元球面S^3の形状そのものということになります。物理学ではスピノールが張られる球空間での3次元回転は複素2次元回転群SU(2)として表されるのですが、実際、このSU(2)の形は3次元球面S^3と同じものとされています。
さて、さて、スピノールが回転している球空間の構造の方はかなりはっきりしてきたのではないかと思います。問題はこの構造が一体何を意味しているのかということです。僕らが何気に暮らしているこの空間の極微領域には現実としてこのような球空間が存在していることを物理学は実証しています。自然は一体なぜ、時空の根底にこのような超ミクロの3次元球面の構造をセットしたのでしょうか。この空間が一体どのような意味を持つ空間なのか、これからヌーソロジーの思考方法で探っていくことにしましょう。ここから、いよいよヌーソロジーが描く異次元世界への旅へと本格的に入っていくことになります。それはトランスフォーマー型ゲシュタルトによる新しい世界観の幕開けとも言っていいものになるでしょう。あっと驚く空間風景が展開してきますよ。お楽しみに。
By kohsen • 時間と別れるための50の方法 • 1 • Tags: トランスフォーマー型ゲシュタルト, メビウス, 人類が神を見る日, 内面と外面, 無限遠