●3次元球面としての知覚球体――魂の皮膚
では、今度は4次元から見たこの次元観察子ψ3とψ4を図を使って、この両者が等化されたところに生じている次元観察子ψ5のカタチを表してみることにしましょう。次元観察子ψ5の球空間の半径は観測者にとっての「前」方向の線分と見なすことができました。そして、その線分は回り回って観測者の後頭部にまで達する線分でした。「正面がうしろ」になるようなこうした線分を前回示した4次元のアナロジー図で表すと次のようになります(下図1参照)。
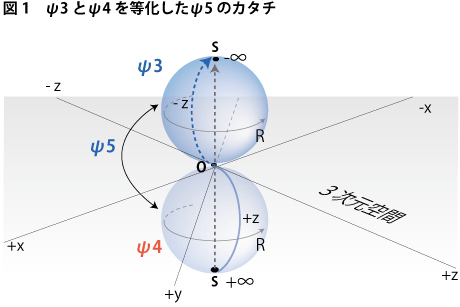
モノの手前方向にある観測者の位置としての+∞の無限遠点から発した矢印がモノの中心である原点Oを貫き、蛇行曲線を描きながら今度はモノの背後方向にある-∞としての無限遠点Sに到達しているのが分ります。このことから、結局のところ、ψ4球面における無限遠点+∞とψ3球面における無限遠点−∞は同じ点Sで重合していることなります。この図ではψ3とψ4それぞれ二つの球面上に表された二つの無限遠点Sは別々のところに描かれていますが、本来は同一の点だということです。
観測者の「前」方向を意味するこの蛇行曲線がψ5の球空間の半径となっているならば、この図に示した球面に沿って回転Rを与えてやれば、点Sを極点とする3次元球面S^3が形作られることになります。このときの回転Rの意味は、図を見れば分かるように、±z方向にあった線分が、±x、±y方向のすべてをなめることができるといったような意味です。
結果的に、回転Rは下図2のように、基底がそれぞれ+1と-1のベクトルを回転させることによって生まれる二つの3次元空間を張り合わさたような形を作り出すことが分かります。基底-1の方をψ3の球空間、+1の方をψ4の球空間と見れば、このψ5は二つの球空間を連続的につなぎ合わせ、その境界を無効にするような意味を持っているわけです。この形が正式な意味での3次元球面S^3です(これを反転させた表示がNCにおける真ん中の球体です)。
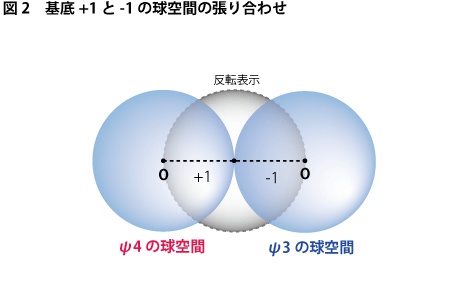
ここで「正式」といったのは、この形になってはじめて3次元球面が多様体としての意味を帯びてくることが予想されるからです。多様体とは簡単にいえば、3次元座標が並進や回転の自由度を持てるようになることをいいます。これは空間が単なる座標から座標系(座標の集まり)に変わるということを意味します。つまり、次元観察子ψ3は単に「3次元の座標」を4次元空間上で丸めたものだったのですが、次元観察子ψ5の方は「3次元の座標系」を丸めたものの意味を持つわけです。
これらの違いをより直観的に思い描くには、上で行った図1に関する説明を次のように変えてみるといいでしょう。図1をもう一度ご覧になって下さい。ψ3とψ4の球面はいわば3次元平面を鏡面とした鏡映のような関係にあります。ならば、観測者の前方向は下図3のような円環でも表せることが分かります。
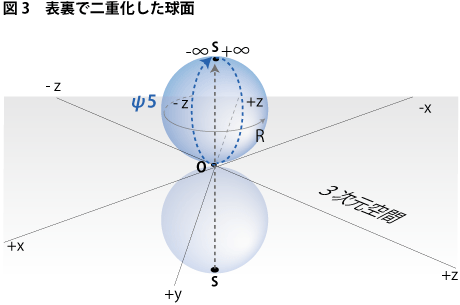
この図3ではψ4球面上で+∞からO点に向かっていたz方向の+の領域をそのままψ3球面の裏面側に移動させて描いただけです。極点Sが+∞と-∞の両方の無限遠点の意味を兼ね備えていることが分かりますね。+∞から原点Oまでは、この球面の裏面側をなぞり、原点Oから-∞まではこの球面の表面側をなぞるような円環としてψ5の球空間の半径部分が表せることが分ります。そして、ここで、この円環に回転Rを与えてみましょう。すると、ψ3球面の表面と裏面とが捩じれた形で繋がっている二重の球面のイメージが形作られてくるはずです。この二重の球面は互いに反転した3次元空間が点Oと∞点で連結し、互いの境界を無効にしている様子を表しています。つまり、二つの3次元の球空間が張り合わされて内面と外面が等化されているわけです。この形を数学的に示すと、正面方向と背後方向がつながった円環S^1に2次元球面S^2を掛け合わせる意味を持った下のような演算になります。
S^1×S^2=S^3(※S^2を底空間とするS^1のファイバー束で全体空間がS^3)
この二重化した球面がなぜ多様体の意味を持つかということを直感的に把握するためには、半径を同じにする二枚の2次元球面を用意するといいでしょう。この二枚の球面を重ね合わせて二重化した2次元球面のイメージを作ります。そして片方の球面をベースとして、もう片方の球面を滑るようにいろいろな方向に回転させてみるのです。2次元球面の中で2次元球面自体がグルグルと様々な方向に回転できるイメージを容易に作れます。このとき、この二枚の球面の次元を一つあげて3次元空間が丸められたものと見なせば、3次元球面という多様体のイメージが、あくまでも比喩的にですが、作れたことになります。3次元の中を3次元が動くイメージです。
さっそく、ここで得たイメージを実際の空間認識に移し替えてみましょう。
たとえば、目の前にある何か一個のモノを見て下さい。そのとき、そのモノから広がる3次元の空間を皆さんはイメージすることができているはずです。それが3次元座標です。そして、次に、その座標自体をイメージの中で前後、左右方向に動かしたり、回転させてみたりして下さい。たぶん、それもイメージが可能なはずです。3次元座標はこのように3次元のどの場所へでもその原点を移動させることができます。こうして、実際、ψ5である観測者の周囲の空間には無数の3次元座標を設定することが可能になることが分ります。こうして設定された3次元座標の集合全体が3次元座標系と呼ばれるものです。
上の説明からいえば、これはψ3の球空間がψ4の球空間の上を動くことによって可能になっているというわけです。つまり、次元観察子ψ3を任意の一つの座標とすれば、そこにψ3×ψ4という形で次元観察子のψ4が掛け合わされることによって、座標の原点自体が3次元の各方向に動けたり、その場で回転できる自由度が生まれてくるということなのです。もっと平たい言い方をすれば、無数のモノを空間に配置することが可能になるということですね。こうしたモノの多数性は、一個のモノから広がる空間内では決して成立しません。なぜなら、3次元上の多数のモノの存在を確認するには、観測者の視線の回転が必要だからです。その意味でも、本来、3次元の座標系というものは観測者から広がる空間において初めて成立すると考える必要があります。3次元空間の多様体としての性質は観察者の存在によって保証されているということです。こうして、観察者にとって一個のモノの観察次元がψ3だったのに対して、無数のモノの観察次元がこのψ5という次元観察子の実際的な意味になります。
まとめておきましょう。一人の観測者から広がっている空間=知覚球体。これは4次元から見ると3次元球面というカタチをとっており、これが次元観察子ψ5となっている――このことをしっかりと覚えておいて下さい。







9月 25 2008
時間と別れるための50の方法(38)
●3次元球面としての知覚球体――魂の皮膚
では、今度は4次元から見たこの次元観察子ψ3とψ4を図を使って、この両者が等化されたところに生じている次元観察子ψ5のカタチを表してみることにしましょう。次元観察子ψ5の球空間の半径は観測者にとっての「前」方向の線分と見なすことができました。そして、その線分は回り回って観測者の後頭部にまで達する線分でした。「正面がうしろ」になるようなこうした線分を前回示した4次元のアナロジー図で表すと次のようになります(下図1参照)。
モノの手前方向にある観測者の位置としての+∞の無限遠点から発した矢印がモノの中心である原点Oを貫き、蛇行曲線を描きながら今度はモノの背後方向にある-∞としての無限遠点Sに到達しているのが分ります。このことから、結局のところ、ψ4球面における無限遠点+∞とψ3球面における無限遠点−∞は同じ点Sで重合していることなります。この図ではψ3とψ4それぞれ二つの球面上に表された二つの無限遠点Sは別々のところに描かれていますが、本来は同一の点だということです。
観測者の「前」方向を意味するこの蛇行曲線がψ5の球空間の半径となっているならば、この図に示した球面に沿って回転Rを与えてやれば、点Sを極点とする3次元球面S^3が形作られることになります。このときの回転Rの意味は、図を見れば分かるように、±z方向にあった線分が、±x、±y方向のすべてをなめることができるといったような意味です。
結果的に、回転Rは下図2のように、基底がそれぞれ+1と-1のベクトルを回転させることによって生まれる二つの3次元空間を張り合わさたような形を作り出すことが分かります。基底-1の方をψ3の球空間、+1の方をψ4の球空間と見れば、このψ5は二つの球空間を連続的につなぎ合わせ、その境界を無効にするような意味を持っているわけです。この形が正式な意味での3次元球面S^3です(これを反転させた表示がNCにおける真ん中の球体です)。
ここで「正式」といったのは、この形になってはじめて3次元球面が多様体としての意味を帯びてくることが予想されるからです。多様体とは簡単にいえば、3次元座標が並進や回転の自由度を持てるようになることをいいます。これは空間が単なる座標から座標系(座標の集まり)に変わるということを意味します。つまり、次元観察子ψ3は単に「3次元の座標」を4次元空間上で丸めたものだったのですが、次元観察子ψ5の方は「3次元の座標系」を丸めたものの意味を持つわけです。
これらの違いをより直観的に思い描くには、上で行った図1に関する説明を次のように変えてみるといいでしょう。図1をもう一度ご覧になって下さい。ψ3とψ4の球面はいわば3次元平面を鏡面とした鏡映のような関係にあります。ならば、観測者の前方向は下図3のような円環でも表せることが分かります。
この図3ではψ4球面上で+∞からO点に向かっていたz方向の+の領域をそのままψ3球面の裏面側に移動させて描いただけです。極点Sが+∞と-∞の両方の無限遠点の意味を兼ね備えていることが分かりますね。+∞から原点Oまでは、この球面の裏面側をなぞり、原点Oから-∞まではこの球面の表面側をなぞるような円環としてψ5の球空間の半径部分が表せることが分ります。そして、ここで、この円環に回転Rを与えてみましょう。すると、ψ3球面の表面と裏面とが捩じれた形で繋がっている二重の球面のイメージが形作られてくるはずです。この二重の球面は互いに反転した3次元空間が点Oと∞点で連結し、互いの境界を無効にしている様子を表しています。つまり、二つの3次元の球空間が張り合わされて内面と外面が等化されているわけです。この形を数学的に示すと、正面方向と背後方向がつながった円環S^1に2次元球面S^2を掛け合わせる意味を持った下のような演算になります。
S^1×S^2=S^3(※S^2を底空間とするS^1のファイバー束で全体空間がS^3)
この二重化した球面がなぜ多様体の意味を持つかということを直感的に把握するためには、半径を同じにする二枚の2次元球面を用意するといいでしょう。この二枚の球面を重ね合わせて二重化した2次元球面のイメージを作ります。そして片方の球面をベースとして、もう片方の球面を滑るようにいろいろな方向に回転させてみるのです。2次元球面の中で2次元球面自体がグルグルと様々な方向に回転できるイメージを容易に作れます。このとき、この二枚の球面の次元を一つあげて3次元空間が丸められたものと見なせば、3次元球面という多様体のイメージが、あくまでも比喩的にですが、作れたことになります。3次元の中を3次元が動くイメージです。
さっそく、ここで得たイメージを実際の空間認識に移し替えてみましょう。
たとえば、目の前にある何か一個のモノを見て下さい。そのとき、そのモノから広がる3次元の空間を皆さんはイメージすることができているはずです。それが3次元座標です。そして、次に、その座標自体をイメージの中で前後、左右方向に動かしたり、回転させてみたりして下さい。たぶん、それもイメージが可能なはずです。3次元座標はこのように3次元のどの場所へでもその原点を移動させることができます。こうして、実際、ψ5である観測者の周囲の空間には無数の3次元座標を設定することが可能になることが分ります。こうして設定された3次元座標の集合全体が3次元座標系と呼ばれるものです。
上の説明からいえば、これはψ3の球空間がψ4の球空間の上を動くことによって可能になっているというわけです。つまり、次元観察子ψ3を任意の一つの座標とすれば、そこにψ3×ψ4という形で次元観察子のψ4が掛け合わされることによって、座標の原点自体が3次元の各方向に動けたり、その場で回転できる自由度が生まれてくるということなのです。もっと平たい言い方をすれば、無数のモノを空間に配置することが可能になるということですね。こうしたモノの多数性は、一個のモノから広がる空間内では決して成立しません。なぜなら、3次元上の多数のモノの存在を確認するには、観測者の視線の回転が必要だからです。その意味でも、本来、3次元の座標系というものは観測者から広がる空間において初めて成立すると考える必要があります。3次元空間の多様体としての性質は観察者の存在によって保証されているということです。こうして、観察者にとって一個のモノの観察次元がψ3だったのに対して、無数のモノの観察次元がこのψ5という次元観察子の実際的な意味になります。
まとめておきましょう。一人の観測者から広がっている空間=知覚球体。これは4次元から見ると3次元球面というカタチをとっており、これが次元観察子ψ5となっている――このことをしっかりと覚えておいて下さい。
By kohsen • 時間と別れるための50の方法 • 0 • Tags: 内面と外面, 無限遠