9月 10 2025
シュレディンガー方程式とは主観空間の数学的表現
シュレディンガー方程式とは、主観空間を数学的に表現したものである。そういう結論になりました。意識が超越論的なものの世界へと侵入していくためのベース基地のようなものです。
例えば、電子の状態ベクトルの回転に対してたえず逆行して働いているのがゲージ場としての電磁場です。それがある意味、エネルギーの固有ベクトルに絶対的な不動性を与え、主観に「いつでも今、どこでもここ」という感覚を与えています。詳しく説明しておきましよう。
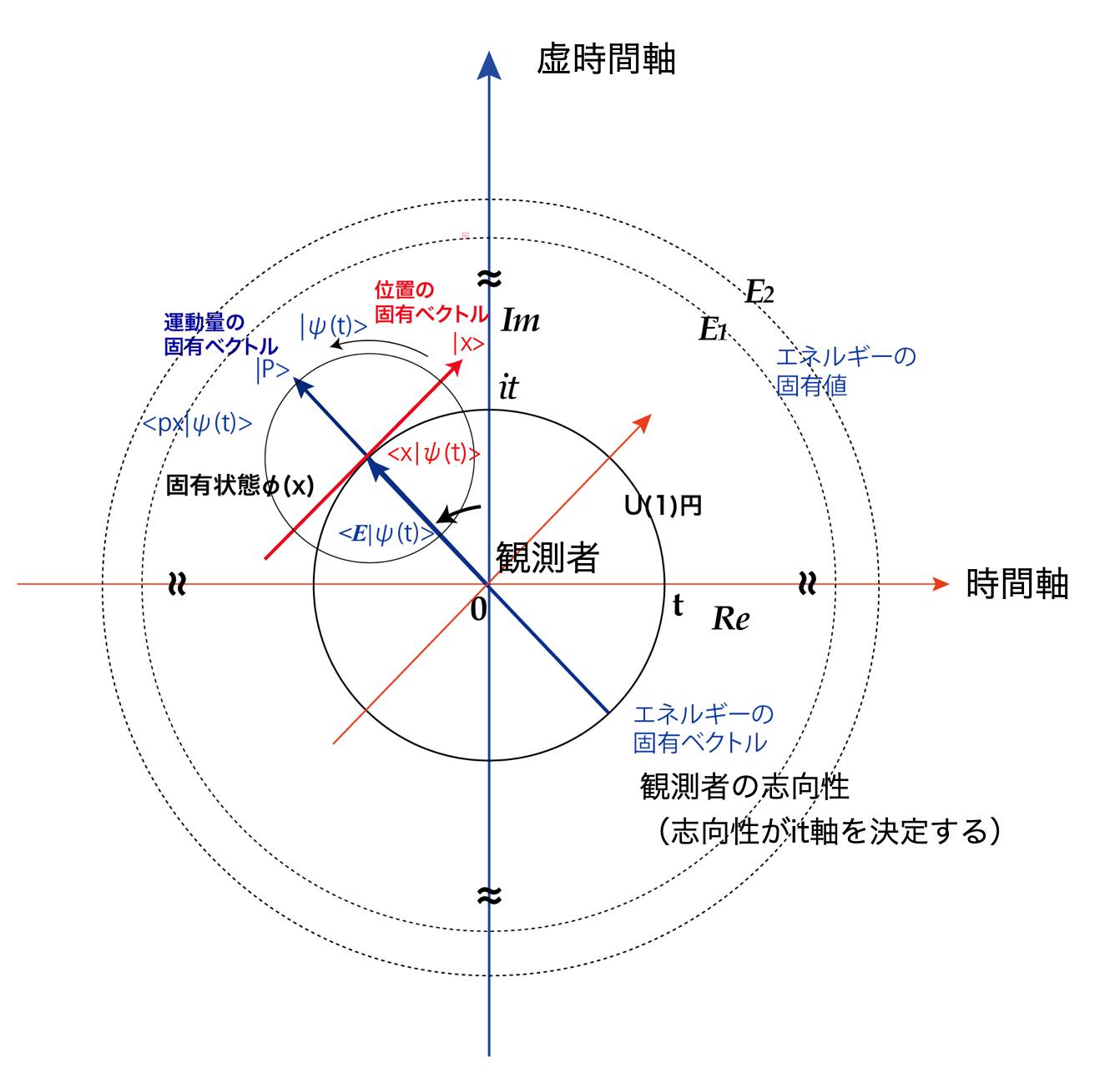
状態ベクトル∣ψ(t)⟩は、シュレディンガー方程式に従って常に回転(時間発展)を続けます。この回転は主観の志向性を表し、意識の持続として感じられます。
一方、ゲージ場(特に電磁場)は、量子力学においてU(1)ゲージ不変性に対応しています。このゲージ場は、状態ベクトルの回転(位相変化)に対して、常に「逆行する方向」へ作用していると解釈することができます。
状態ベクトルは主観的な志向性として時間に沿って進行(回転)しようとして行きます。しかし、電磁場(ゲージ場)はその回転に対して常に「逆方向のベクトル」を与え、その進行を相殺し、一定の「基準となる方向」を示し続けます。この二つの働きが相補的に作用しているわけです。
ゲージ場(電磁場)が常に逆向きの作用を与えていることは、意識が常に参照できる絶対的な「基準軸」の生成に繋がります。これはエネルギー固有ベクトル ∣E⟩に特別な不動性を与えています。
つまり、状態ベクトルと電磁場(ゲージ場)、この二者が対照的に働き合い、主観空間の中においてエネルギー(認識)方向に「不動点」を作り出すことで、「いつでも今、どこでもここ」という絶対的な意識の安定感(不動性・持続性)が得られているということです。
自分の周りに、このような不可視の空間メカニズムが働いているということを知ることは、とても面白いですよ。それがあるから、君に君というものが感じられている。量子世界というものは物理的対象なんかではないということ。
昨日「いや、見るとは、世界を生成している起点そのものなのだ」「 世界の始まりは対象ではなく、持続の自覚にある。」って書いたけど、今話したことが、この「持続の自覚」に当たると思ってください。
主観(見ること)が客観(見られること)を断ち切って、生成の世界へと入っていく始まりの位置のようなものです。
魂の中へと入っていく方法論というのは古今東西たくさん伝承されてきたんだろうけど、OCOT情報ではそれは反転した思考によって達成されないといけないと言っていた。ようやく、それが実現する時代がやってきたんじゃないかなって、個人的には思ってる。







9月 11 2025
量子の詩
θshellさん作曲
シュレーディンガー方程式ヌーソロジー解釈 「量子の詩 – いつも、ここにある不思議」- NOOSAI Maki
https://suno.com/song/e82f28f9-5dd9-4f66-9bd5-0e496b27e0b1
Perfumeとかに歌わせたいですね。合います(笑)
By kohsen • 01_ヌーソロジー, 07_音楽 • 0 • Tags: シュレディンガー方程式